WebGL

  1. Introduction
  2. Pipeline de rendu
  3. Vertex buffers
  4. Shaders
  5. Divers
  6. Adaptation d'un sketch Processing
  7. Post-traitement

Introduction

Interface de programmation en JavaScript pour le rendu 2D/3D adaptée aux accélérateurs graphiques (GPU)

Expose OpenGL ES 2.0 / 3.0 via un contexte de rendu associé à un élément HTML canvas

Historique:

  • 1992: OpenGL 1.0
  • 2004: OpenGL 2.0, introduction des shaders
  • 2007: OpenGL ES 2.0, smartphones, tablettes, consoles, etc...
  • 2011: WebGL 1.0, basé sur OpenGL ES 2.0
  • 2011: WebGL 1.0 disponible dans Firefox 4, Chrome 9 et Safari 5.1
  • 2011: WebGL 1.0 disponible dans Internet Explorer 11
  • 2012: OpenGL ES 3.0, rétro-compatible avec OpenGL ES 2.0
  • 2017: WebGL 2.0, basé sur OpenGL ES 3.0
  • 2017: WebGL 2.0 disponible dans Firefox 51 et Chrome 56

Introduction

Point de départ: récupérer un contexte WebGL (HTML5 Canvas)

Code HTML

Code JavaScript


              var canvas = document.getElementById('canvas');
              var gl = canvas.getContext('webgl');

              if (!gl)
                return;

              // Call WebGL methods gl.*

Pipeline de rendu

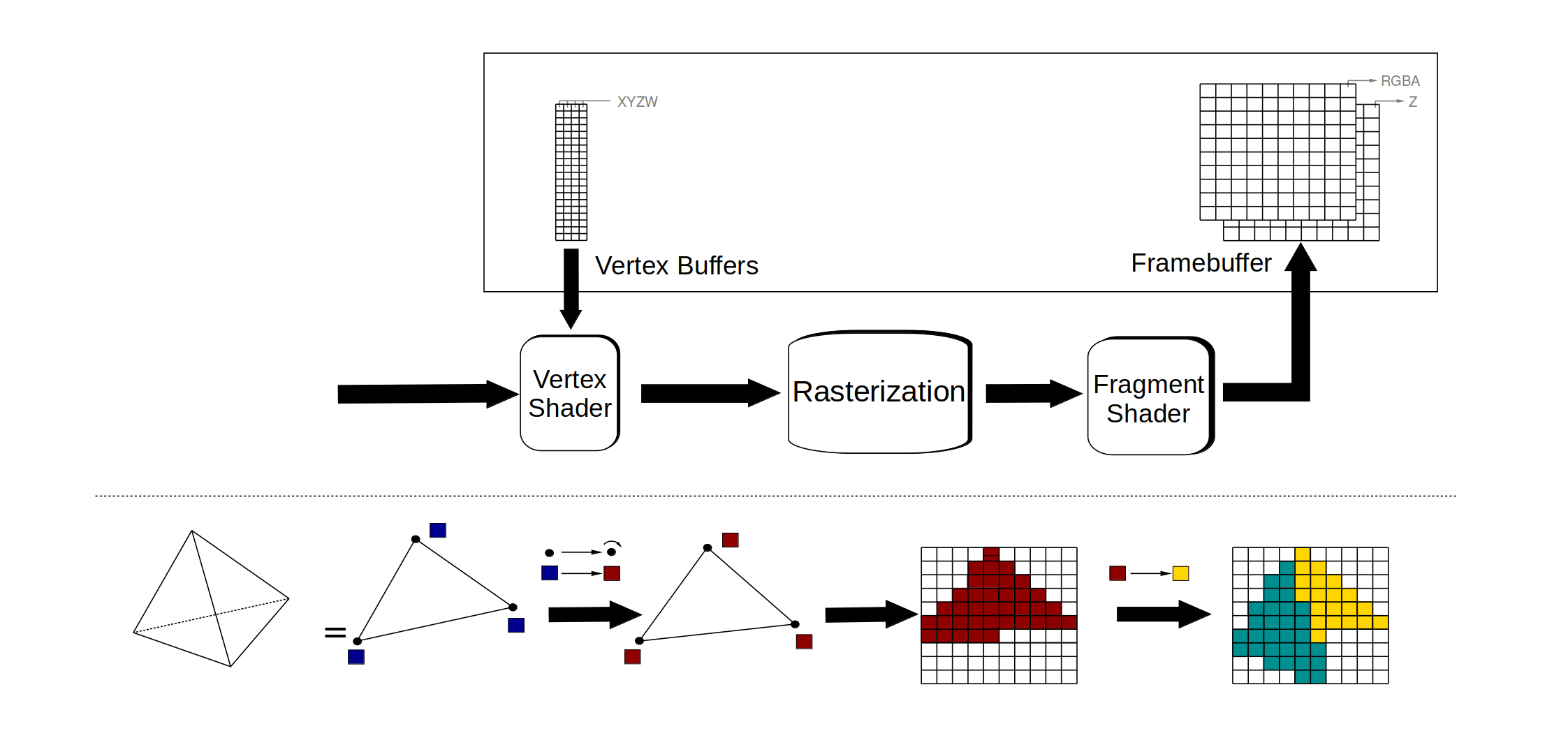
Vertex buffers - Création

Géométrie stockée dans des vertex buffers

(tableaux de données résidant en mémoire du GPU)


              var positions = [
                  // 2 triangles for +z face
                  -1.0, -1.0,  1.0, 
                   1.0, -1.0,  1.0, 
                   1.0,  1.0,  1.0, 

                  -1.0, -1.0,  1.0, 
                   1.0,  1.0,  1.0, 
                  -1.0,  1.0,  1.0, 
                  // ...
              ];
              var positionArray = new Float32Array(positions);

              var positionBuffer = gl.createBuffer();
              gl.bindBuffer(gl.ARRAY_BUFFER, positionBuffer);
              gl.bufferData(gl.ARRAY_BUFFER, positionArray, gl.STATIC_DRAW)
              gl.bindBuffer(gl.ARRAY_BUFFER, null);

À rapprocher de beginShape() / endShape() en Processing

Vertex buffers - Utilisation

Type de géométrie (triangles, bande de triangles, points, lines) spécifié lors de l'appel à la fonction de rendu DrawArrays()


              var numVertices = positions.length / 3;

              gl.DrawArrays(gl.TRIANGLES, 0, numVertices);

Shaders

Vertex shader
Programme pour calculer la position finale d'un vertex (vertex shader)

Fragment shader
Programme pour calculer la couleur finale d'un pixel parcouru lors de la rastérization (fragment shader)

Shaders écrits avec un langage de programmation dédié: GLSL ES

Shaders - GLSL ES

Syntaxe dérivée du C

Additions majeures:

  • Types et opérations pour vecteurs / matrices de faible dimensions: vec(2|3|4), mat(2|3|4)
  • Opération d'extraction des composantes: vec3(1.0, 2.0, 3.0).zy
  • Qualificateurs d'argument de fonction: in, out, inout
  • Fonctions: mathématiques (sin, cos, ..., clamp, mix, smoothstep) et autres (distance, cross, reflect, ...)
  • Variables de type attribute (vertex), uniform (globale) et varying (interpolée)
  • Variable de sortie: gl_Position (vertex), gl_FragCoord (fragment)
  • Point d'entrée: main()

Shaders - GLSL ES

Limitations:

  • Environment d'exécution très limité
  • Tableaux à une dimension seulement
  • Taille et indexage des tableaux avec expression constante
  • Expression constante pour le nombre d'itérations dans une boucle
  • ...

Shaders - Vertex shaders

Exemple de vertex shader:

Transformation de position et copie de normale

Code GLSL


              attribute vec3 aPosition;
              attribute vec3 aNormal;

              uniform mat4 uProjectionMatrix;
              uniform mat4 uModelViewMatrix;

              varying vec3 vNormal;

              void main() {
                  gl_Position = uProjectionMatrix * uModelViewMatrix * vec4(aPosition, 1.0);
                  vNormal = aNormal;
              }

Shaders - Fragment Shader

Exemple de fragment shader: modèle simplifié d'illumination

Code GLSL


              precision highp float;

              varying vec3 vNormal;

              uniform vec3 uAmbient;
              uniform vec3 uDiffuse;
              uniform vec3 uLightVector;

              void main() {
                  vec3 color = uAmbient;
                  color += uDiffuse * max(dot(vNormal, normalize(uLightVector)), 0.0);
                  gl_FragColor = vec4(color, 1.0);
              }

Shaders - Création

Compiler un vertex shader à partir du code GLSL sous forme de chaîne de charactère (shaderSource)

Code WebGL


              var vertexShader = gl.createShader(gl.VERTEX_SHADER);
              // Use gl.FRAGMENT_SHADER for fragment shaders

              gl.shaderSource(vertexShader, shaderSource);
              gl.compileShader(vertexShader);

              if (!gl.getShaderParameter(vertexShader, gl.COMPILE_STATUS)) {
                  console.log(gl.getShaderInfoLog(vertexShader));
                  // ...
              }

Shaders - Édition de liens

Lier un vertex shader et un fragment shader

en un shader program utilisable avec le pipeline de rendu

Code WebGL


              var program = gl.createProgram();
              gl.attachShader(program, vertexShader);
              gl.attachShader(program, fragmentShader);
              gl.linkProgram(program);

              if (!gl.getProgramParameter(program, gl.LINK_STATUS)) {
                  console.log(gl.getProgramInfoLog(program));

                  // ...
              }

              gl.useProgram(program);

Shaders - Attributs de vertex et variables uniformes

Attributs de vertex

Code WebGL


                gl.bindBuffer(gl.ARRAY_BUFFER, positionBuffer);

                var location = gl.getAttribLocation('aPosition');
                gl.enableVertexAttribArray(location);
                gl.vertexAttribPointer(location, 3, gl.FLOAT, false, 0, 0);

Variables uniformes

Code WebGL


                var projectionMatrix = [ /* ... */ ];
                var location = gl.getUniformLocation('uProjectionMatrix');
                gl.uniformMatrix4fv(location, false, projectionMatrix);

Divers

Code JavaScript


              function setup() {
                // ...
                gl.clearColor(0.0, 0.0, 0.0, 1.0);
                gl.enable(gl.DEPTH_TEST);
                // ...
              }

              function draw() {
                gl.viewport(0, 0, WIDTH, HEIGHT);
                gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);
                // ...
              }

Gestion d'évènements et animation

Code JavaScript


              window.addEventListener('mousemove', handleMouse, false);
              // ...
              window.requestAnimationFrame(canvas, animationLoop);

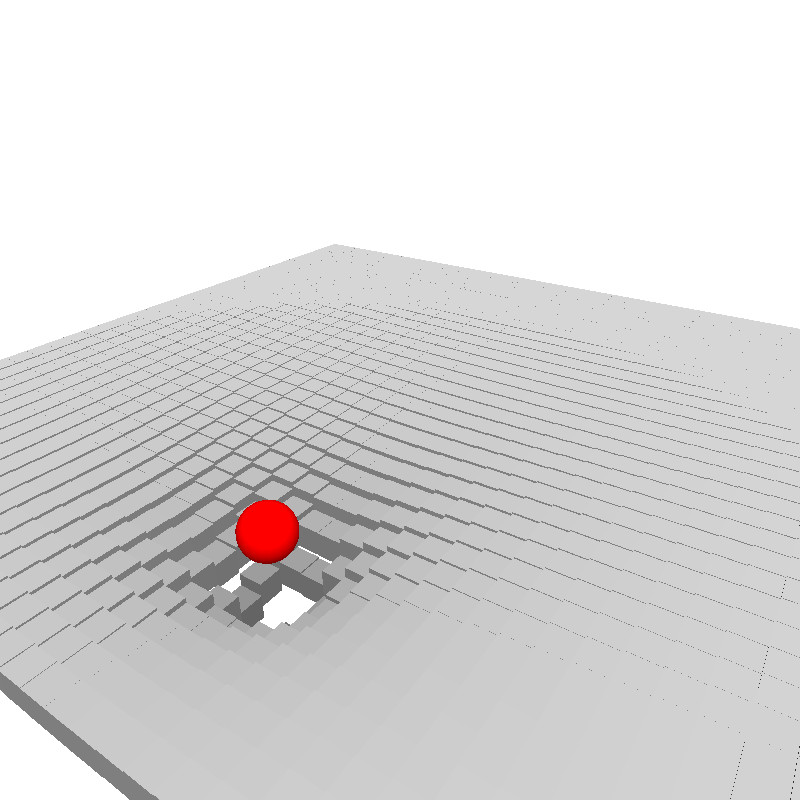
Adaptation d'un sketch Processing

3D Gravity Well (Marvin K)

Portage simple WebGL:

  • Caméra:
    • rotation, translation, projection via une classe Matrix4x4
    • variable uniforme pour la projection / transformation finale
  • Géométrie:
    • génération explicite de triangles pour sphère et cube
    • vertex buffers pour position et normale
  • Matériaux et illumination:
    • variable uniforme pour les matériaux et la source de lumière
    • calcul d'illumination dans le fragment shader

Taille du code:

  • Processing.js: ~ 60 LoC
  • WebGL + GLSL: ~ 800 LoC

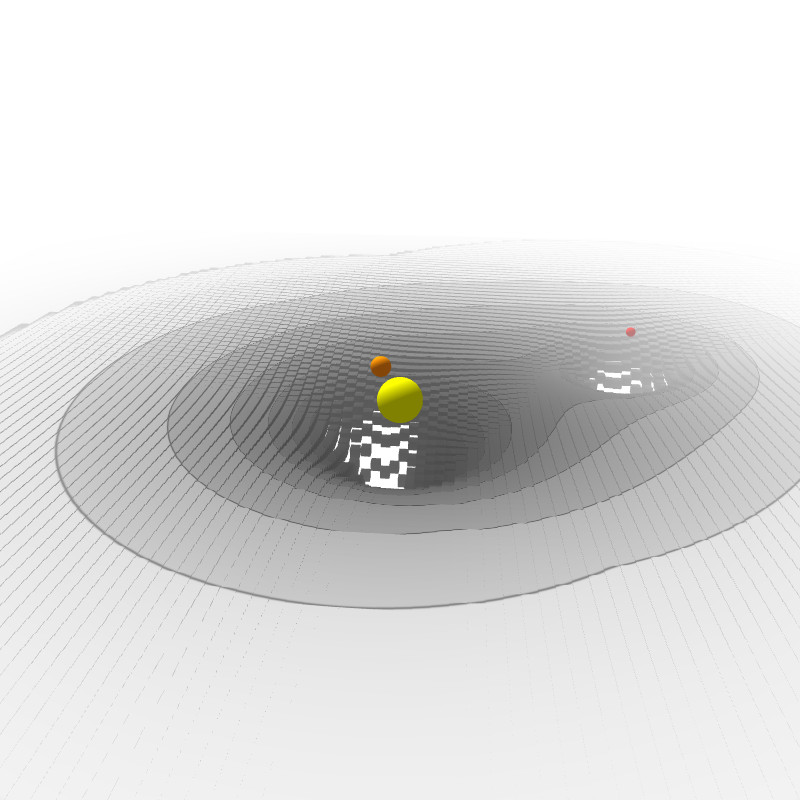
Adaptation d'un sketch Processing

3D Gravity Well (Marvin K)

Adaption d'un sketch Processing

3D Gravity Well (Marvin K)

Améliorations possibles en WebGL:

  • Anticrénelage: activer l'option antialias
  • Plus de géométrie:
    • Activer le filtrage des faces vues de dos (backface culling)
    • Un seul vertex buffer pour stocker position + normal
  • (Encore) plus de géométrie:
    • Calcul d'élévation réalisé dans le vertex shader
  • Couleur fonction de l'élévation
  • Tracé des lignes de niveau de l'élévation
  • Post-traitement: brouillard (masque les limites de la grille)

Post-traitement: brouillard (fog)

Améliore la perception de la profondeur

`C_(p ixel)^' = (1 - t) C_(p ixel) + t C_(fog)`

`t = 1 - e^(-(rho d)^2)`

avec `d`: distance camera-oeil-origine / point de la scène,

et `rho`: densité de brouillard


Alternatives:

`t = (d - d_min) / (d_max - d_min)` ou `t = 1 - e^(-rho d)`


Références